The Bethe Ansatz

Let us now do the converse of the above: we construct an excited state by now punching a hole in the \(N\) particle ground state, choosing the quantum numbers

\begin{equation*} \{ I_j \} = \left\{ -\frac{N}{2} + 1, ..., \frac{N}{2} - m - 1, \frac{N}{2} - m + 1, ..., \frac{N}{2} \right\}. \end{equation*}

We single out the \(I^0 = \frac{N - 1}{2} - m\) quantum number in the ground state interval (viewing \(m\) as being in \(0 < m < \frac{N}{2}\), namely the hole is on the right side of the Fermi interval) and call the associated rapidity \(q\) with restriction \(|q| < \lambda_F\). We therefore have to order \(1/L\)

\begin{equation*} d_j = \pi + \phi (\lambda_j - q) - \frac{1}{L} \sum_{l=1}^{N-1} \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2} (d_j - d_l) \end{equation*}

which leads to the following equation for the corresponding displacement:

\begin{equation} D_h (\lambda, q) - \int_{-\lambda_F}^{\lambda_F} d\lambda' {\cal C}(\lambda-\lambda') D_h(\lambda',q) = \frac{1}{2\pi} \left( \pi + \phi(\lambda - q) \right), \hspace{5mm} \lambda \in [-\lambda_F, \lambda_F], ~ 0 < q < \lambda_F. \tag{l.d2}\label{l.d2} \end{equation}

The change in momentum can be expressed as

\begin{equation} \Delta P = -q + \sum_{l=1}^{N-1} (\lambda_j - \lambda^0_j) = -q + \sum_{l=1}^{N-1} \Delta \lambda_j = -q + \int_{-\lambda_F}^{\lambda_F} d\lambda D_h (\lambda, q) \tag{l.d2p}\label{l.d2p} \end{equation}

whilst the change in energy is

\begin{equation} \Delta E = -q^2 + \mu + \sum_{l=1}^{N-1} (\lambda_j^2 - {\lambda_j^0}^2) = -q^2 + \mu + 2 \int_{-\lambda_F}^{\lambda_F} d\lambda \lambda D_h(\lambda, q). \tag{l.d2e}\label{l.d2e} \end{equation}

The type II dipsersion relation is illustrated in Fig. fig-T2disprel for various values of the interaction parameter.

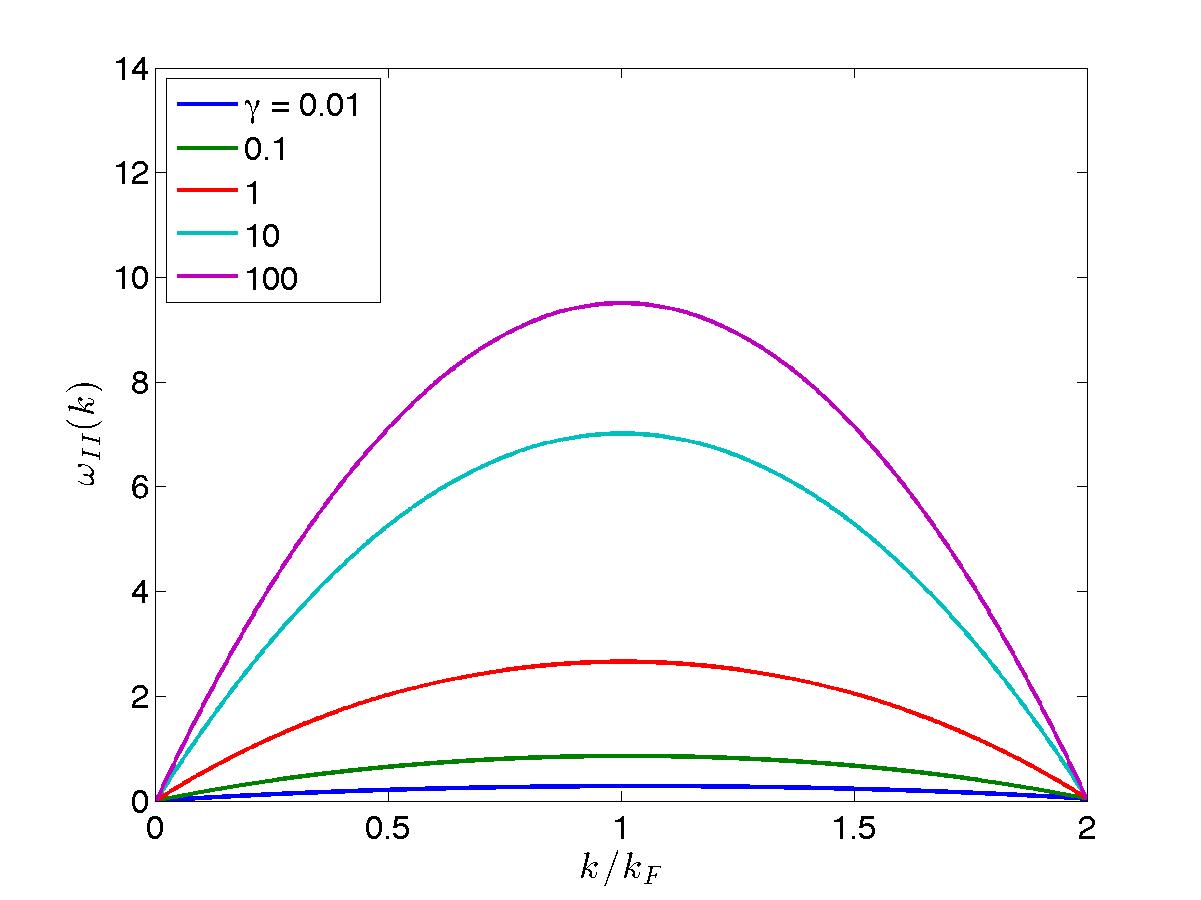
In the limit \(c \rightarrow 0^+\), we get \(\epsilon(p) = 0\).

For \(c \rightarrow \infty\), the solution is \(D_h = 1/2\), so \(\Delta P = - q + \lambda_F\) and \(\Delta E = -q^2 + \mu\). Since \(\mu = \lambda_F^2\) and \(\lambda_F = \pi n\), we obtain in this case

\begin{equation*} \epsilon(p) = -p^2 + 2\pi n p, \hspace{0.3cm} c \rightarrow \infty, \hspace{5mm} p \in [0, 2 \pi n]. \end{equation*}

These two limits form the lower and upper limits of the hole-like excitations.